Double-Slit
Interference and Single-Slit Diffraction Experiments on Electrons
Huawang
Li
Abstract: De Broglie
proposed the matter wave in 1924. The de Broglie wave is neither a mechanical
wave nor an electromagnetic (EM) wave and has a very short wavelength. The
Davisson-Germer electron diffraction experiment performed in 1925 involved
bombarding the surface of a nickel crystal with a narrow beam of electrons.
When the accelerating voltage V was maintained at 54 V, the wavelength of the incident
electron was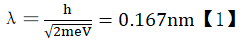 , demonstrating the existence of the matter wave. We
introduce a type of electron wave with a very long wavelength in this study that
is different from the matter wave. For example, the wavelength of the electron
wave can reach 0.43 mm in the double-slit interference of electrons. Experiments
demonstrate that this long-wavelength electron wave can produce both
double-slit interference and electron diffraction. A comparative analysis of
matter and electron waves reveals the physical natures of these waves and
wave–particle duality.
, demonstrating the existence of the matter wave. We
introduce a type of electron wave with a very long wavelength in this study that
is different from the matter wave. For example, the wavelength of the electron
wave can reach 0.43 mm in the double-slit interference of electrons. Experiments
demonstrate that this long-wavelength electron wave can produce both
double-slit interference and electron diffraction. A comparative analysis of
matter and electron waves reveals the physical natures of these waves and
wave–particle duality.
Keywords: Double-slit electron interference, Electron diffraction,
Wave-particle duality
Introduction
The
discovery of long-wavelength electron interference and diffraction follows from
multiple hypotheses. (1) The universe is filled with a gas of particles with an
average kinetic energy equal to the Planck constant. This gas particle is
referred to as a Yizi, [2], and the gas is called a Yizi gas. (2) Light
is transmitted by the Yizi gas. As the average speed of a Yizi is approximately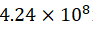 m/s, the speed of light in a Yizi gas is
m/s, the speed of light in a Yizi gas is m/s. (3) The moving mass of electrons and
protons is equal to the static mass of these particles plus the mass of the
Yizi gas displaced by these particles. The mass-energy equivalence is E = 1/2 ×
the mass of the Yizi gas displaced by electrons or protons × the square of the
average speed of a Yizi. (4) Like protons, electrons and Yizi particles have
point spherical surfaces that are both concave and convex. Particles participate
in edge-edge collisions, that is, linear momentum and angular momentum are
transferred at the same time. Protons, electrons, and Yizi particles undergo
linear motion and eccentric rotation, and the motion trajectory of the center of
mass (COM) in the respective rotational plane is a circular closed curve composed
of periodic fluctuation curves, as shown in Figure 1. The linear motion of electrons
from left to right is accompanied by eccentric rotation around Point P
m/s. (3) The moving mass of electrons and
protons is equal to the static mass of these particles plus the mass of the
Yizi gas displaced by these particles. The mass-energy equivalence is E = 1/2 ×
the mass of the Yizi gas displaced by electrons or protons × the square of the
average speed of a Yizi. (4) Like protons, electrons and Yizi particles have
point spherical surfaces that are both concave and convex. Particles participate
in edge-edge collisions, that is, linear momentum and angular momentum are
transferred at the same time. Protons, electrons, and Yizi particles undergo
linear motion and eccentric rotation, and the motion trajectory of the center of
mass (COM) in the respective rotational plane is a circular closed curve composed
of periodic fluctuation curves, as shown in Figure 1. The linear motion of electrons
from left to right is accompanied by eccentric rotation around Point P
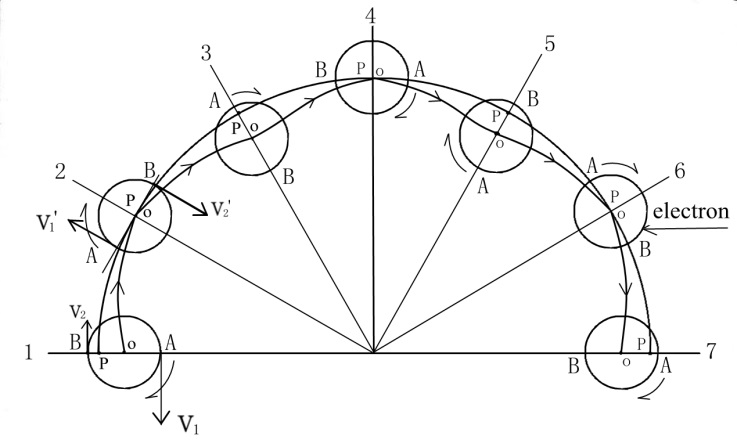
Points A
and B in the figure are two mass points with the same mass on the electron
surface. At Position 1, the linear velocity of Point A in eccentric rotation around Point P is greater
than the linear velocity
of Point A in eccentric rotation around Point P is greater
than the linear velocity of Point B rotating around Point
P, such that Point A has a higher angular momentum than Point B. During the
eccentric rotation of electrons, the angular momentum of Point A is gradually transferred
to Point B, and vice versa. Point A, upon reaching Position 2, has the same
angular momentum as Point B, and the center of rotation, Point P, coincides
with the COM, Point O. When Point B reaches Position 3, the linear velocity of Point
B rotating around Point P changes to
of Point B rotating around Point
P, such that Point A has a higher angular momentum than Point B. During the
eccentric rotation of electrons, the angular momentum of Point A is gradually transferred
to Point B, and vice versa. Point A, upon reaching Position 2, has the same
angular momentum as Point B, and the center of rotation, Point P, coincides
with the COM, Point O. When Point B reaches Position 3, the linear velocity of Point
B rotating around Point P changes to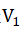 , and the linear velocity of Point A rotating around Point P changes
to
, and the linear velocity of Point A rotating around Point P changes
to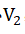 , that is, in moving from Position 1 to Position 3, Point A exchanges
angular momentum with Point B. This continuous exchange of angular momentum
provides a periodically varying centripetal force with a period greater than or
equal to zero, such the trajectory of the COM of the electron in the respective
rotation plane is a circular closed curve composed of periodic fluctuation
curves. Macroscopic objects are composed of many elementary particles. In a
rotating macroscopic object, these particles can transfer angular momentum to
each other, where the even distribution of the angular momentum around the COM
enables the macroscopic object to rotate around the COM. The eccentric rotation
of protons, electrons, and Yizi particles determines the polarization of the
particles and ensures that all particles in the universe do not fly out of
space. (5) The universe is composed of a large but finite number of elementary
particles and is therefore limited in size. The electromagnetic (EM) waves
emitted by all the celestial bodies reverberate in the size-limited universe, resulting
in a cosmic background temperature of 2.73 K. (6) High-speed particles are
subject to the resistance of the Yizi gas and therefore exhibit a large moving
mass. At present, dozens of particles with different masses are only
superluminal electrons generated by the collision of electrons with high-speed
protons. (7) The magnetic field is a cyclone generated by a static or flowing
Yizi gas. Particles in a magnetic field are deflected in a direction that
depends on the frequency of EM waves generated by particle motion. The EM waves
in the Yizi cyclone have a natural frequency. Moving particles with frequencies
that are the same as or close to the natural frequency of the magnetic field
are repelled by the EM wave. Moving particles with frequencies different from
the natural frequency of the magnetic field are attracted by the EM wave. (8)
When a large-mass particle and a small-mass particle collide elastically at
equal and opposite velocities, the resulting velocity of the small-mass
particle is higher than that of the large-mass particle. Therefore, the smaller
the masses of the elementary particles in the universe, the higher the average particle
velocity is. For example, the velocity of electrons can exceed
, that is, in moving from Position 1 to Position 3, Point A exchanges
angular momentum with Point B. This continuous exchange of angular momentum
provides a periodically varying centripetal force with a period greater than or
equal to zero, such the trajectory of the COM of the electron in the respective
rotation plane is a circular closed curve composed of periodic fluctuation
curves. Macroscopic objects are composed of many elementary particles. In a
rotating macroscopic object, these particles can transfer angular momentum to
each other, where the even distribution of the angular momentum around the COM
enables the macroscopic object to rotate around the COM. The eccentric rotation
of protons, electrons, and Yizi particles determines the polarization of the
particles and ensures that all particles in the universe do not fly out of
space. (5) The universe is composed of a large but finite number of elementary
particles and is therefore limited in size. The electromagnetic (EM) waves
emitted by all the celestial bodies reverberate in the size-limited universe, resulting
in a cosmic background temperature of 2.73 K. (6) High-speed particles are
subject to the resistance of the Yizi gas and therefore exhibit a large moving
mass. At present, dozens of particles with different masses are only
superluminal electrons generated by the collision of electrons with high-speed
protons. (7) The magnetic field is a cyclone generated by a static or flowing
Yizi gas. Particles in a magnetic field are deflected in a direction that
depends on the frequency of EM waves generated by particle motion. The EM waves
in the Yizi cyclone have a natural frequency. Moving particles with frequencies
that are the same as or close to the natural frequency of the magnetic field
are repelled by the EM wave. Moving particles with frequencies different from
the natural frequency of the magnetic field are attracted by the EM wave. (8)
When a large-mass particle and a small-mass particle collide elastically at
equal and opposite velocities, the resulting velocity of the small-mass
particle is higher than that of the large-mass particle. Therefore, the smaller
the masses of the elementary particles in the universe, the higher the average particle
velocity is. For example, the velocity of electrons can exceed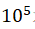 m/s, and the velocity of a Yizi
can exceed
m/s, and the velocity of a Yizi
can exceed m/s. (9) An additional
interesting phenomenon is observed. When the mass M of a particle is considerably
larger than the mass m of a different particle and the effect of the particle volumes
is neglected, the momentum of the large-mass particle is equal to that of the small-mass
particle, i.e.,Mv=mV ①.
m/s. (9) An additional
interesting phenomenon is observed. When the mass M of a particle is considerably
larger than the mass m of a different particle and the effect of the particle volumes
is neglected, the momentum of the large-mass particle is equal to that of the small-mass
particle, i.e.,Mv=mV ①.
Then, the velocity V of the small-mass particle
is considerably higher than the velocity v of the large-mass particle, i.e.,
whenM≫m,v≪V ②.
From ① and ②, , that is, the large-mass particle is in a very low temperature
state, and the small-mass particle is in a very high temperature state. Consider
that the small- and large-mass particles have equal kinetic energies, i.e.,
, that is, the large-mass particle is in a very low temperature
state, and the small-mass particle is in a very high temperature state. Consider
that the small- and large-mass particles have equal kinetic energies, i.e.,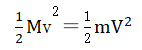 ③.
③.
From ② and ③,Mv≫mV, and both particles are in a
very high temperature state.
The abovementioned
phenomenon shows that when two elementary particles with different masses are
mixed together, the momenta of the two particles tend to equalize, and the
temperature of the large-mass particle is lower than that of the small-mass
particle. At this point, if these two elementary particles of different masses
are completely separated, the large-mass particle can absorb the energy of the
small-mass particle until the temperatures of the two particles equalize, such
that the kinetic energies of the two particles tend to equalize.
Similarly,
the temperature of a proton in a mixture of many protons and many Yizi
particles is not the same as that when these protons and Yizi particles are
completely separated. When a single proton suspended in a Yizi gas collides
with the surrounding Yizi particles, the proton momentum tends to become equal to
the average momentum of the Yizi particles, i.e.,Mz×Vz≈My×Vy ④.
The mass
of the proton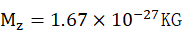 , the mass of Yizi
, the mass of Yizi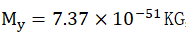 , and the average velocity
of Yizi
, and the average velocity
of Yizi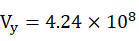 m/s. The average velocity
of the proton can be obtained from ④ as
m/s. The average velocity
of the proton can be obtained from ④ as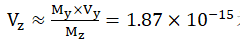 m/s, and the corresponding
proton temperature is close to absolute zero. If the mass densities of the protons,
electrons, and Yizi particles are the same, the volume of a proton could be
m/s, and the corresponding
proton temperature is close to absolute zero. If the mass densities of the protons,
electrons, and Yizi particles are the same, the volume of a proton could be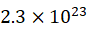 times that of the
Yizi. Therefore, the influence of the proton volume must be considered when
many protons collect together and are completely separated from the Yizi gas
that fills cosmic space. Each proton can absorb the kinetic energy of the Yizi particles
in the Yizi gas, whereby the kinetic energy of each proton becomes equal to the
sum of the kinetic energies of N Yizi particles, i.e.,
times that of the
Yizi. Therefore, the influence of the proton volume must be considered when
many protons collect together and are completely separated from the Yizi gas
that fills cosmic space. Each proton can absorb the kinetic energy of the Yizi particles
in the Yizi gas, whereby the kinetic energy of each proton becomes equal to the
sum of the kinetic energies of N Yizi particles, i.e.,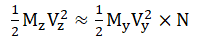 ⑤,
where N is equal to the frequency of gamma rays produced by the self-collision
of protons. If the frequency of gamma rays
⑤,
where N is equal to the frequency of gamma rays produced by the self-collision
of protons. If the frequency of gamma rays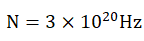 , then the average velocity of the proton
from ⑤
is
, then the average velocity of the proton
from ⑤
is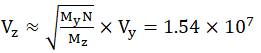 m/s.
m/s.
In this case, the
temperature of the proton is equal to the central temperature of the sun, the
central temperature of the earth, and the temperature in an atomic nucleus with
a large atomic weight. The center of the sun and the center of the earth, like
the nucleus of an atom, are made of protons. In fact, the nuclei of solid
matter emit gamma rays at every moment, but most of the energy of the gamma
rays is absorbed by the outer electrons of the nucleus, which release this energy
in the form of thermal radiation. The use of X- and γ-ray meters to determine
the air-kerma rate of the solid matter shows that all the solid matter around
us always radiates X- and γ-rays at dose rates generally below0.25μSv/h. A Yizi transfers kinetic energy to protons via direct collision,
which is then released as EM waves to maintain a dynamic balance. The cosmic
space is not empty but full of Yizi gas. The energy of the Yizi gas per unit
space volume is [3], that is, the
cosmic space is full of energy. We do not feel this energy because there is no
energy difference between our bodies and cosmic space, where all the energy in
the universe is kinetic energy. The Yizi gas contains an enormous quantity of energy
and is at a super-high pressure. Fish in deep water do not feel hydrostatic pressure,
and birds that land on high-voltage transmission lines do not feel electricity;
similarly, we also do not feel the enormous energy and super-high pressure in
space. (10) The high-pressure Yizi gas squeezes multiple protons into an atomic
nucleus and constrains electrons to remain at the surface of this nucleus. The
number of electrons outside the atomic nucleus is mainly related to the surface
area of the nucleus, i.e., the larger the surface area of the nucleus is, the more
electrons can be bound. Electrons and protons do not possess electricity. If this
hypothesis is correct, there should be a wavelength associated with the
fluctuation curve of an electron. Electrons could produce double-slit
interference and single-slit diffraction just like visible light, but the fluctuations
of the electrons should produce an electron wave with a wavelength much longer than
the wavelength of the matter wave of electrons, for which experimental evidence
is presented in the following sections.
[3], that is, the
cosmic space is full of energy. We do not feel this energy because there is no
energy difference between our bodies and cosmic space, where all the energy in
the universe is kinetic energy. The Yizi gas contains an enormous quantity of energy
and is at a super-high pressure. Fish in deep water do not feel hydrostatic pressure,
and birds that land on high-voltage transmission lines do not feel electricity;
similarly, we also do not feel the enormous energy and super-high pressure in
space. (10) The high-pressure Yizi gas squeezes multiple protons into an atomic
nucleus and constrains electrons to remain at the surface of this nucleus. The
number of electrons outside the atomic nucleus is mainly related to the surface
area of the nucleus, i.e., the larger the surface area of the nucleus is, the more
electrons can be bound. Electrons and protons do not possess electricity. If this
hypothesis is correct, there should be a wavelength associated with the
fluctuation curve of an electron. Electrons could produce double-slit
interference and single-slit diffraction just like visible light, but the fluctuations
of the electrons should produce an electron wave with a wavelength much longer than
the wavelength of the matter wave of electrons, for which experimental evidence
is presented in the following sections.
1. Two experiments on the wave properties of electrons
1.1. Double-slit
interference experiment on long-wavelength electrons
1.1.1. Equipment:
(1) Vacuum tank: internal diameter, 180 cm; internal height, 180 cm; and material,
steel plate. (2) Molecular pumps for generating a vacuum up to Pa. (3) Negative direct current (DC) high-voltage
power supply: high voltages up to -30,000 V and currents up to 1.4 mA. (4) Cathode
emission source: a 3-mm-diameter stainless steel rod. (5) Two slits are made in
a 20-cm-long, 15-cm-wide, and 0.5-mm-thick plastic plate. The width and length of
the slits are 3 mm and 10 cm, respectively, and the distance between the two
slits is 4 mm. The plastic plate is embedded in a 90-cm-wide, 120-cm-high, and
2-mm-thick organic glass plate. (6) An interferometry fringe display screen:
one side is a plexiglass plate, and the other side is a steel ruler connected
to the ground. Figure 2 shows the setup of the double-slit interference and
single-slit diffraction experiments.
Pa. (3) Negative direct current (DC) high-voltage
power supply: high voltages up to -30,000 V and currents up to 1.4 mA. (4) Cathode
emission source: a 3-mm-diameter stainless steel rod. (5) Two slits are made in
a 20-cm-long, 15-cm-wide, and 0.5-mm-thick plastic plate. The width and length of
the slits are 3 mm and 10 cm, respectively, and the distance between the two
slits is 4 mm. The plastic plate is embedded in a 90-cm-wide, 120-cm-high, and
2-mm-thick organic glass plate. (6) An interferometry fringe display screen:
one side is a plexiglass plate, and the other side is a steel ruler connected
to the ground. Figure 2 shows the setup of the double-slit interference and
single-slit diffraction experiments.

Figure
2 Setup
of the electron double-slit interference and single-slit diffraction
experiments
|
1.1.2. Experimental
principle: The electrons emitted by the cathode emission source can be regarded
as wave sources with the same vibration direction, the same frequency, and a
constant phase difference. The principle for obtaining fringes of coherent
electrons and wavelength measurement is shown in Figure 3.
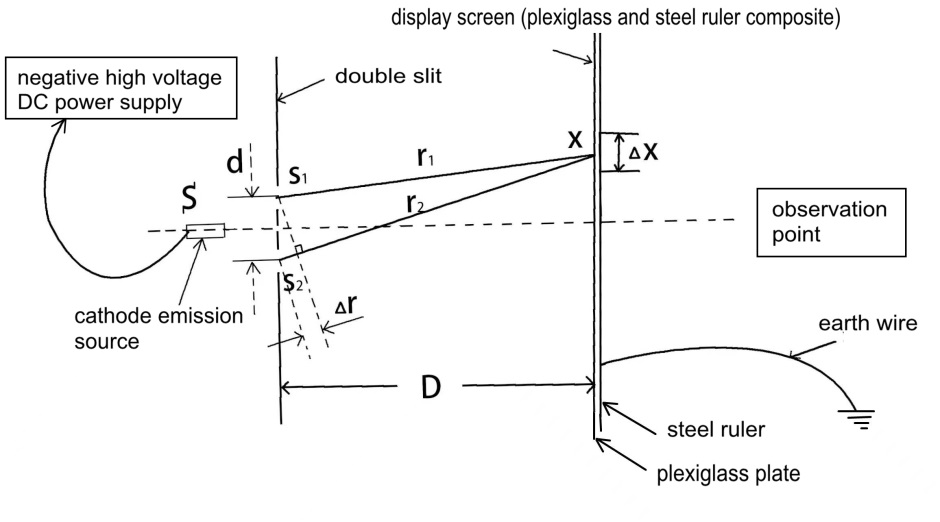
Figure 3 Principle of
double-slit electron interference
|
The cathode source S
emits electrons with a wavelength of λ that pass through the double slits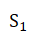 and
and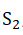 with a spacing d. Some of
these electrons hit the plexiglass plate of the display screen, and other
electrons are absorbed by the steel ruler behind the organic glass, forming an
interference pattern at the upper edge of the steel ruler. The distance between
the interference fringes is denoted as ∆x, and the
distance between the double slits and the display screen is denoted as D. Then,
the wavelength of the electron wave is approximately
with a spacing d. Some of
these electrons hit the plexiglass plate of the display screen, and other
electrons are absorbed by the steel ruler behind the organic glass, forming an
interference pattern at the upper edge of the steel ruler. The distance between
the interference fringes is denoted as ∆x, and the
distance between the double slits and the display screen is denoted as D. Then,
the wavelength of the electron wave is approximately 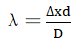 [4].
[4].
1.1.3. Experimental procedure: (1) The
cathode emission source, the plastic plate with double slits, and the display
screen made of plexiglass plate and steel ruler are placed in sequence in a
vacuum tank. (2) The steel ruler is connected to the ground, and the vacuum
tank is closed. (3) The vacuum pump is turned on. When the absolute pressure in
the vacuum tank reaches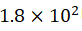 Pa, the negative DC high-voltage power supply
is turned on. When the voltage reaches -1710 V (U=1710 V) and
the current reaches -1.23 mA, the cathode emission source starts to emit stable
cathode rays. (4) The electrons emitted by the cathode source pass through the
double slits. Some electrons hit the plexiglass plate of the screen, and some
electrons bypass the organic glass and are absorbed by the steel ruler to
create an interference pattern at the upper edge of the steel ruler, as shown
in Figure 4.
Pa, the negative DC high-voltage power supply
is turned on. When the voltage reaches -1710 V (U=1710 V) and
the current reaches -1.23 mA, the cathode emission source starts to emit stable
cathode rays. (4) The electrons emitted by the cathode source pass through the
double slits. Some electrons hit the plexiglass plate of the screen, and some
electrons bypass the organic glass and are absorbed by the steel ruler to
create an interference pattern at the upper edge of the steel ruler, as shown
in Figure 4.
|

Figure
4 Double-slit electron interference pattern
|
(5) Data and
results: Given the simple test setup, only a qualitative analysis is conducted.
The distance between the two slits is d = 7 mm, the distance between the two
slits and the steel ruler is D = 400 mm, and the average distance between
interference fringes is ∆x = 24.3 mm; hence,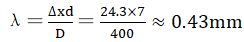 .
.
The
determined wavelength is not very accurate but nevertheless, quite different
from the wavelength of matter waves. Changing the vacuum degree does not affect
the fringes, indicating that the electrons have an inherent wave.
Neglecting the energy lost by
electrons during wire transmission yields the kinetic energy of the electrons
emitted from the cathode emission source as , where m is the electron mass,
, where m is the electron mass,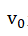 is the linear velocity of
the electrons after escaping from the cathode emission source, e is the electron
charge, U is the voltage applied to the cathode emission source, and W is the
work function required for electrons to escape from the cathode emission source.
Neglecting W, which is usually small (e.g., typically, the metal work function
is the linear velocity of
the electrons after escaping from the cathode emission source, e is the electron
charge, U is the voltage applied to the cathode emission source, and W is the
work function required for electrons to escape from the cathode emission source.
Neglecting W, which is usually small (e.g., typically, the metal work function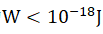 ), changes the formula presented above to
), changes the formula presented above to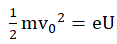 , where
, where
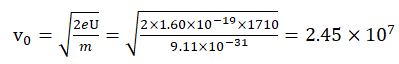 m/s, the propagation speed
of an electron wave
m/s, the propagation speed
of an electron wave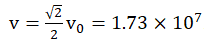 m/s, and the frequency of
an electron wave
m/s, and the frequency of
an electron wave .
.
1.2. Single-slit
diffraction experiment of electrons with a long wavelength
1.2.1. Equipment:
(1) Vacuum tank: internal diameter, 180 cm; internal height, 180 cm; and material,
steel plate. (2) Molecular pumps for generating a vacuum up to Pa. (3) Negative DC high-voltage
power supply: high voltages up to -30,000 V and currents up to 1.4 mA. (4) Cathode
emission source S: an Al nail with an 8-mm cap diameter. (5) A 5-mm-wide single
slit is engraved on a plexiglass plate with a width of 90 cm, a height of 120
cm and a thickness of 2 mm. (6) A diffraction fringe screen: one side is a strip-shaped
plexiglass plate, and the other side is a steel ruler connected to the ground.
Pa. (3) Negative DC high-voltage
power supply: high voltages up to -30,000 V and currents up to 1.4 mA. (4) Cathode
emission source S: an Al nail with an 8-mm cap diameter. (5) A 5-mm-wide single
slit is engraved on a plexiglass plate with a width of 90 cm, a height of 120
cm and a thickness of 2 mm. (6) A diffraction fringe screen: one side is a strip-shaped
plexiglass plate, and the other side is a steel ruler connected to the ground.
1.2.2. Experimental
principle: The electrons emitted by the cathode emission source can be regarded
as wave sources with the same vibration direction, the same frequency, and a
constant phase difference. Figure 5 shows the principle used to obtain the
first-order dark fringe of the diffraction fringes and measure the wavelength.
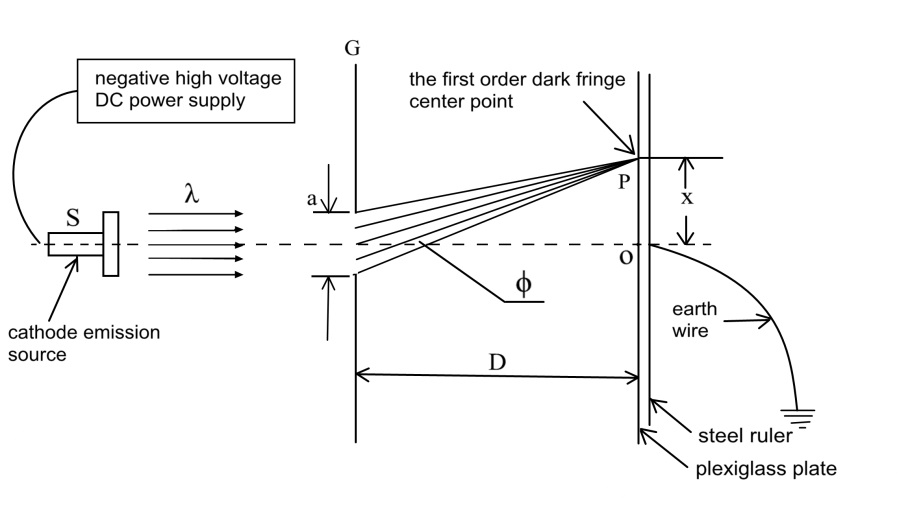
Figure 5 Schematic of single
slit diffraction
|
The cathode emission source
S emits electrons with a wavelength λ that pass through the single slit G with
spacing a. Some electrons hit the plexiglass plate of the display screen, and some
electrons bypass the plexiglass plate and are absorbed by the steel ruler
behind the plexiglass plate to create a diffraction pattern on the upper edge
of the steel ruler. The distance from the center of the first dark fringe to
the central axis is denoted as x, the diffraction angle is denoted asϕ, the distance from the single slit to the display screen is denoted
as D, and the wavelength of the electron wave is approximately
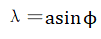 [5],
[5],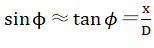 ,
,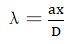 .
.
1.2.3. Experimental procedure
(1) The
cathode emission source, the plexiglass
plate with a single slit, and the display
screen made of the plexiglass plate and steel ruler are placed in sequence in a
vacuum tank. The plexiglass plate with a single slit is approximately 10 cm
from the cathode emission source and 360 mm from the display screen. (2) The
steel ruler is connected to the ground, and the vacuum tank is closed. (3) The
vacuum pump is turned on. When the absolute pressure in the vacuum tank reaches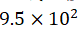 Pa, the vacuum pump is turned off, and the
negative DC high-voltage power supply is turned on. The voltage is slowly
increased until the cathode emission source emits a stable cathode ray (the
voltage reaches -2260 V (U = 2260 V) and
the current reaches -0.7 mA). (4) The electrons pass through the single slit,
some of which hit the organic glass on the display screen, and some which are
absorbed by the steel ruler behind the organic glass. A diffraction pattern is
formed at the upper edge of the steel ruler, as shown in Figures 6
and 7 (which show patterns obtained at night and during the day, respectively).
Pa, the vacuum pump is turned off, and the
negative DC high-voltage power supply is turned on. The voltage is slowly
increased until the cathode emission source emits a stable cathode ray (the
voltage reaches -2260 V (U = 2260 V) and
the current reaches -0.7 mA). (4) The electrons pass through the single slit,
some of which hit the organic glass on the display screen, and some which are
absorbed by the steel ruler behind the organic glass. A diffraction pattern is
formed at the upper edge of the steel ruler, as shown in Figures 6
and 7 (which show patterns obtained at night and during the day, respectively).

Figure 6 Single-slit electron
diffraction pattern (obtained at night)
|

Figure 7 Single-slit electron
diffraction pattern (obtained during the day) at absolute pressure = 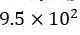 Pa, U = -2260 V,
and I = -0.7 mA Pa, U = -2260 V,
and I = -0.7 mA
|
(5) Data and results: The
width of the single slit is a = 5 mm, the distance from the single slit to the
display screen is D = 360 mm, and the distance from the center of the first
dark fringe to the central axis is x ≈ 35 mm; thus,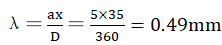 . Given the simple test setup, the determined wavelength is not
very accurate and is used only as a reference.
. Given the simple test setup, the determined wavelength is not
very accurate and is used only as a reference.
The linear velocity of the electrons that have escaped from the cathode
emission source m/s. The electron wave has
a propagation speed
m/s. The electron wave has
a propagation speed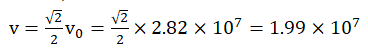 m/s and a frequency
m/s and a frequency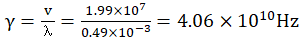 .
.
(6) Increasing the vacuum in the vacuum tank causes the voltage to
drop rapidly and the current to increase rapidly. As the allowable working
current of the high-voltage DC power supply is ≤ 1.4 mA, the voltage of the
high-voltage DC supply must be constantly reduced during the vacuum process to prevent
the occurrence of an overcurrent. The vacuum pump is turned off when the
absolute pressure in the vacuum tank reaches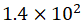 Pa. At this moment, the
voltage is -920 V (U = 920 V) and the current is -0.62 mA: the diffraction
pattern of the electrons on the display screen is shown in Figure 8.
Pa. At this moment, the
voltage is -920 V (U = 920 V) and the current is -0.62 mA: the diffraction
pattern of the electrons on the display screen is shown in Figure 8.

(7) Data and results: The
width of a single slit is a = 5 mm, the distance from the single slit to the
display screen is D = 360 mm, and the distance from the center of the first
dark fringe to the central axis is x ≈ 31 mm; thus, . Given the simple test setup, the determined wavelength is not
very accurate and is used only as a reference.
. Given the simple test setup, the determined wavelength is not
very accurate and is used only as a reference.
The linear velocity of the electrons that have escaped from the cathode
emission source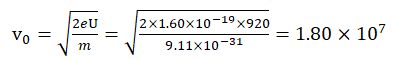 m/s. The electron wave has
a propagation speed
m/s. The electron wave has
a propagation speed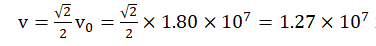 m/s and a frequency
m/s and a frequency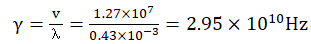 . Both the wavelength and
frequency of the electron wave decrease as the voltage decreases.
. Both the wavelength and
frequency of the electron wave decrease as the voltage decreases.
(8) Maintaining the absolute
pressure at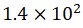 Pa, the current is
increased to 1.30 mA, resulting in a voltage of 1010 V. The electron
single-slit diffraction pattern (obtained during the day) is shown in Figure 9.
Pa, the current is
increased to 1.30 mA, resulting in a voltage of 1010 V. The electron
single-slit diffraction pattern (obtained during the day) is shown in Figure 9.

Figure 9 Single-slit electron
diffraction pattern (obtained during the day) at U = 1010 V and I = 1.30 mA
|
Comparing Figures 8 and 9
shows that a small increase in the voltage does not result in a significant
change in the diffraction fringes even for a 2.1-fold increase in the current.
If the frequency of an electron wave depends on the current, a 2.1-fold
increase in the current should double the frequency of the electron wave. Thus,
this experiment shows that the current has no effect on the single-slit
diffraction of electrons.
(9) Figures 7 and 8 show
that a decrease in the pressure in the vacuum tank from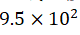 Pa to
Pa to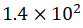 Pa does not result in a
noticeable change in the diffraction fringes, indicating that the density of the
residual gas does not affect the single-slit diffraction of electrons.
Pa does not result in a
noticeable change in the diffraction fringes, indicating that the density of the
residual gas does not affect the single-slit diffraction of electrons.
2. Experimental considerations
(1) The optimal slit width in both the double-slit
interference and single-slit diffraction experiments ranges from 3 mm to 5 mm.
(2) When the absolute pressure in the vacuum tank is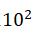 -
-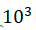 Pa, clear fringes are observed in
the double-slit interference and single-slit diffraction experiments.
The absolute pressure should not be too small. At absolute pressures below 16
Pa, the electrons emitted by the cathode emission source can diffuse like a
gas, and a cathode ray cannot be produced. (3) In both the double-slit
interference and single-slit diffraction experiments, both double and single
slits should be embedded in a large insulating plate to prevent the cathode rays
from bypassing the double or single slit to reach the display screen.
Pa, clear fringes are observed in
the double-slit interference and single-slit diffraction experiments.
The absolute pressure should not be too small. At absolute pressures below 16
Pa, the electrons emitted by the cathode emission source can diffuse like a
gas, and a cathode ray cannot be produced. (3) In both the double-slit
interference and single-slit diffraction experiments, both double and single
slits should be embedded in a large insulating plate to prevent the cathode rays
from bypassing the double or single slit to reach the display screen.
3. Conclusions
(1) The physical meaning of the matter wave is
as follows. Simply speaking, when an object moves in a gas, a matter wave is generated
as a fluctuation due to the continuous resistance of the particles constituting
the gas, that is, a matter wave is a probability wave. When an object moves in a
Yizi gas, EM waves are generated, and the object itself moves forward in a
wavelike manner. The kinetic energy of an object represents the ability of
electrons to occupy a space (volume). A fixed quantity of energy can be
contained in a unit volume of space. The higher the kinetic energy of an
object, the more volume the object occupies in space, the higher the number of
collisions with Yizi particles per unit time is, the shorter the wavelength of
the matter wave is, and the higher the frequency of the matter wave is. Figure
10 shows the idealized trajectory of an electron. However, a probability wave
is generated by the collision between the electrons
moving in a Yizi gas and the Yizi particles. Transforming the equation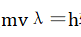 to
to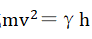 and letting
and letting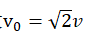 yields
yields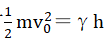 .
.
In the formulas given
above, m is the mass of an electron; v is the wave velocity of the electron matter wave; λ is the wavelength of the matter
wave; h is Planck’s constant, i.e., the average kinetic energy of the Yizi
particles; γ is the frequency of the matter wave, which represents the number
of Yizi particles in the collision; and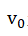 is the average speed of the electrons. The
velocity v in the mass wave equationmvλ=h is
not equal to the average velocity
is the average speed of the electrons. The
velocity v in the mass wave equationmvλ=h is
not equal to the average velocity of the moving particle: instead,
of the moving particle: instead,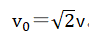 . The Yizi gas interferes with the
motion of electrons, resulting in the generation of matter waves, the
uncertainty principle [6], and the difference between the moving
mass and static mass.
. The Yizi gas interferes with the
motion of electrons, resulting in the generation of matter waves, the
uncertainty principle [6], and the difference between the moving
mass and static mass.

Figure
10 Idealized trajectory of an electron
|
(2) An electron wave is generated by the
periodic curvilinear motion of the eccentric rotation of an electron. This
eccentric rotation prevents electrons from moving uniformly and linearly in the
absence of an external force (e.g., such as that exerted by macroscopic objects) and
results in the wave-particle duality of electrons.
The most significant feature of electron waves
is that the wavelength and frequency of the electron increase simultaneously
with the velocity.
(3) A characteristic common
to both the electron matter wave and electron wave is that the wavelength and
frequency are independent of the current.
(4) The wavelength measured
in the double-slit interference and the single-slit diffraction experiments in
this study is 0.43 mm and 0.49 mm, respectively. By comparison, in the 1925 Davisson-Germer
electron diffraction experiment, the wavelength of the matter wave of an incident
electron was measured asλ=0.167 nm. Taking double-slit interference as an example, the wavelength of
the electron wave is approximately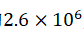 times the wavelength of the
matter wave, that is, the wavelengths of the electron wave and matter wave are
not on the same order of magnitude.
times the wavelength of the
matter wave, that is, the wavelengths of the electron wave and matter wave are
not on the same order of magnitude.
The matter wave and electron wave have completely different
properties. The matter wave is the fluctuation generated by the collision of a
moving object with Yizi gas particles and incorporates everything moving in the
Yizi gas, including the object. The electron wave is unique to elementary
particles and results from the eccentric rotation of electrons. Macroscopic
objects do not undergo eccentric rotation and therefore cannot form this unique
wave.
References
[1]
Y. S. Chen, Z. Z. Li, College Physics (Tianjin University, Tianjin, 1999).
[2] H.W. Li, Physics
Essays 34. 2, 236 (2021).
DOI: https://doi.org/10.4006/0836-1398-34.2.236
[3] H. W. Li, Physics
Essays 34. 2, 236 (2021).
DOI: https://doi.org/10.4006/0836-1398-34.2.236
[4] Y. S. Chen,
Z. Z. Li, College Physics (Tianjin
University, Tianjin, 1999).
[5] Y. S. Chen,
Z. Z. Li, College Physics (Tianjin
University, Tianjin, 1999).
[6] Y. S. Chen, Z.
Z. Li, College Physics (Tianjin
University, Tianjin, 1999).

